函数依赖

总述

函数依赖，提到这个概念我们有时候分不清楚它的关系，总结是一个将知识转化为自己东西的一个方法。现在咱们一起来”分解“它：函数依赖。

分述

一、函数依赖关系

1.数据依赖 数据依赖通常包括函数依赖和多值依赖。

2.函数依赖问题

A.函数依赖
定义：
设一个关系R，X和Y是它的两个属性集，若对于X上的每一个值都有Y上的一个唯一的值与之对应，则称X和Y 具有函数依赖关系，并称X函数决定Y，或称Y函数依赖X，称X为决定因素。
简而言之：一个X值只对应一个Y值。
e.g设一个学生关系为（学号，姓名，性别，）
学生号为该关系的主键
每一个学生的学生号对应着姓名属性的唯一值，即一个学生的姓名由其学生的学号唯一确定，在这里，我们称学号函数决定姓名，或称姓名函数依赖职工号。

B.部分函数依赖
定义：
设一个关系R，X和Y是它的两个属性集，若X函数决定Y，同时X的一个子集X也能够函数决定Y,则称Y部分函数依赖于X
简而言之：只拿出X属性集的一部分，就可以函数决定Y了，不需要全部属性。
e.g如上面的例子：设一个学生关系为（学号，姓名，性别，）
学生号是一个单值属性决定因素，它决定其他的么一个属性，如果把（学生号，姓名）看成X，它能够决定其他所有属性，而职工号一个属性就能够函数决定其他属性，所以（学生号，姓名）到其他属性间的函数依赖为部分函数依赖 。

C.传递函数依赖
定义：
一个关系R，X,Y和Z是它的三个属性集，其中X→Y，Y→Z（Y不包含Z，X也不函数依赖Y），则存在X→Z,称此为传递函数依赖，即X传递函数依赖决定Y，Y传递函数依赖于Z。
简而言之：这个函数依赖关系是通过“推导”间接得到的。

e.g设一个学生关系为（学号，姓名，性别，系号，系名，系主任名）
由题我们知道：学号→系号，系号→系名，所以知道一个学号之后就能够唯一对应一个系号，系号又能确定唯一的一个系名，所以学号→系名，这个关系为传递函数依赖。

二.图形概括 eg.设一个学生关系（学号，姓名，性别，班级，班主任，课程号，课程名，考试成绩）则用函数依赖关系可以如下表示： 注：一个学生属于一个班，一个班有多名学生，一个班级有一个班主任，一个班主任只带一个班。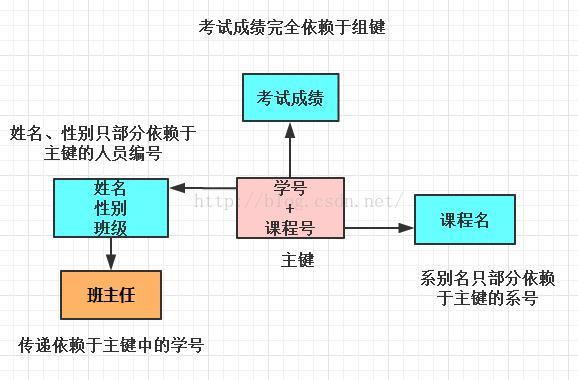

关系模式函数依赖 关系数据库逻辑设计 针对具体问题，如何构造一个适合于它的数据模式 数据库逻辑设计的工具──关系数据库的规范化理论 关系模式由五部分组成，即它是一个五元组：
R(U, D, DOM, F)
R： 关系名
U： 组成该关系的属性名集合
D： 属性组U中属性所来自的域
DOM： 属性向域的映象集合
F： 属性间数据的依赖关系集合

数据依赖

一个关系内部属性与属性之间的约束关系 现实世界属性间相互联系的抽象 数据内在的性质 语义的体现 2. 数据依赖的类型 函数依赖（Functional Dependency，简记为FD） 多值依赖（Multivalued Dependency，简记为MVD） 其他
关系模式R（U, D, DOM, F）
简化为一个三元组：
R（U, F）
当且仅当U上的一个关系r满足F时，r称为关系模式 R（U, F）的一个关系
数据依赖对关系模式的影响
[例1]建立一个描述学校教务的数据库：
学生的学号（Sno）、所在系（Sdept）
系主任姓名（Mname）、课程名（Cname）
成绩（Grade）
单一的关系模式 ： Student <U、F>
U ＝｛ Sno, Sdept, Mname, Cname, Grade ｝

属性组U上的一组函数依赖F：
F ＝｛ Sno → Sdept, Sdept → Mname,
(Sno, Cname) → Grade ｝
关系模式Student(U, F)中存在的问题 1. 数据冗余太大 2. 更新异常（Update Anomalies） 3. 插入异常（Insertion Anomalies） 4. 删除异常（Deletion Anomalies） 结论： Student关系模式不是一个好的模式。 “好”的模式： 不会发生插入异常、删除异常、更新异常， 数据冗余应尽可能少 原因：由存在于模式中的某些数据依赖引起的（这也是对关系 模式进行分解的根本理由） 解决方法：通过分解关系模式来消除其中不合适的数据依赖

分解关系模式

把这个单一模式分成3个关系模式：
S（Sno，Sdept，Sno → Sdept）;
SC（Sno，Cno，Grade，（Sno，Cno） → Grade）;
DEPT（Sdept，Mname，Sdept→ Mname）

规范化

规范化理论正是用来改造关系模式，通过分解关系模式来消除其中不合适的数据依赖，以解决插入异常、删除异常、更新异常和数据冗余问题。
最终使各关系模式达到某种程度的分离，即“一事一地”的模式设计原则

函数依赖

函数依赖（Functional Dependency,FD） 平凡函数依赖与非平凡函数依赖 完全函数依赖与部分函数依赖 传递函数依赖
设R(U)是一个属性集U上的关系模式，X和Y是U的子集。
若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等， 而在Y上的属性值不等， 则称 “X函数确定Y” 或 “Y函数依赖于X”，记作X→Y。

设有关系模式R（U），X和Y是属性集U的子集，函数依赖（functional dependency，简记为FD）是形为X→Y的一个命题，若对于R(U)的任意一个可能的关系r ，对r中任意两个元组t和s，都有t［X］＝s［X］蕴涵 t［Y］＝s［Y］，那么称FD X→Y在关系模式R（U）中成立。
1、所有关系实例均要满足 2、语义范畴的概念

平凡函数依赖与非平凡函数依赖

在关系模式R(U)中，对于U的子集X和Y，
如果X→Y，但Y  X，则称X→Y是非平凡的函数依赖
若X→Y，但Y  X, 则称X→Y是平凡的函数依赖
例：在关系SC(Sno, Cno, Grade)中，
非平凡函数依赖： (Sno, Cno) → Grade
平凡函数依赖： (Sno, Cno) → Sno
(Sno, Cno) → Cno

若X→Y，则X称为这个函数依赖的决定属性组，也称为决定因素（Determinant）。
若X→Y，Y→X，则记作X←→Y。
若Y不函数依赖于X，则记作X→Y。

完全函数依赖与部分函数依赖

在R(U)中，如果X→Y，并且对于X的任何一个真子集X’，都有X’ Y, 则称Y对X完全函数依赖，记作
X F Y。
若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作X P Y。

[例1] 中(Sno,Cno)→Grade是完全函数依赖，
(Sno,Cno)→Sdept是部分函数依赖
因为Sno →Sdept成立，且Sno是（Sno，Cno）的真子集

传递函数依赖

在R(U)中，如果X→Y，(Y X) ,Y→X Y→Z，Z ∈Y, 则称Z对X传递函数依赖。
记为：X → Z

注: 如果Y→X， 即X←→Y，则Z直接依赖于X。

例: 在关系Std(Sno, Sdept, Mname)中，有：
Sno → Sdept，Sdept → Mname
Mname传递函数依赖于Sno